• We consider a Peridynamic simulation of Glass material using RNP Peridynamic model (Regularized Nonlinear Peridynamic) developed and studied in Lipton 2016 and Jha and Lipton 2018. RNP model is implemented in class RNPBond.

  • Units are SI units, e.g. length is in meter, mass is in kg, force is in N, and time is in second.

  • Elastic properties of material are as follows:

    • Bulk modulus K = 25.0E+09 Pa
    • Poisson ratio $\nu$ = 0.25
    • Density $\rho$ = 1200 kg/$m^3$

  • Fracture properties of material are as follows:

    • Critical energy release rate $G_c$ = 500 J/$m^2$

  • For above elastic properties and fracture properties, we can compute the parameters in Peridynamic material model. This has been described in detail in RNPBond::computeParameters.

  • Material domain is rectangle with length $L_x$ = 0.1 m in x-direction and length $L_y$ = 0.1 m in y-direction. We use plane-stress assumption and take thickness of material to be just 1 m.

  • Horizon is $\epsilon$ = $L_y$/50 and mesh size is h = $\epsilon$/4.

  • Time domain

    • Final time T = 0.00014
    • Time steps N = 35000
    • Output frequency of simulation data: N/70

  • Boundary condition

    • We fix top layer of thickness, i.e. we apply displacement boundary condition $u_x$ = 0 and $u_y$ = 0.

    • We apply constant velocity (i.e. linear in time displacement) on layers at the bottom edge of domain. The thickness of layer is same as horizon $\epsilon$.

    • Value of constant velocity along x-direction is v = 1.0 m/s.

    • Displacement boundary condition is implemented in ULoading

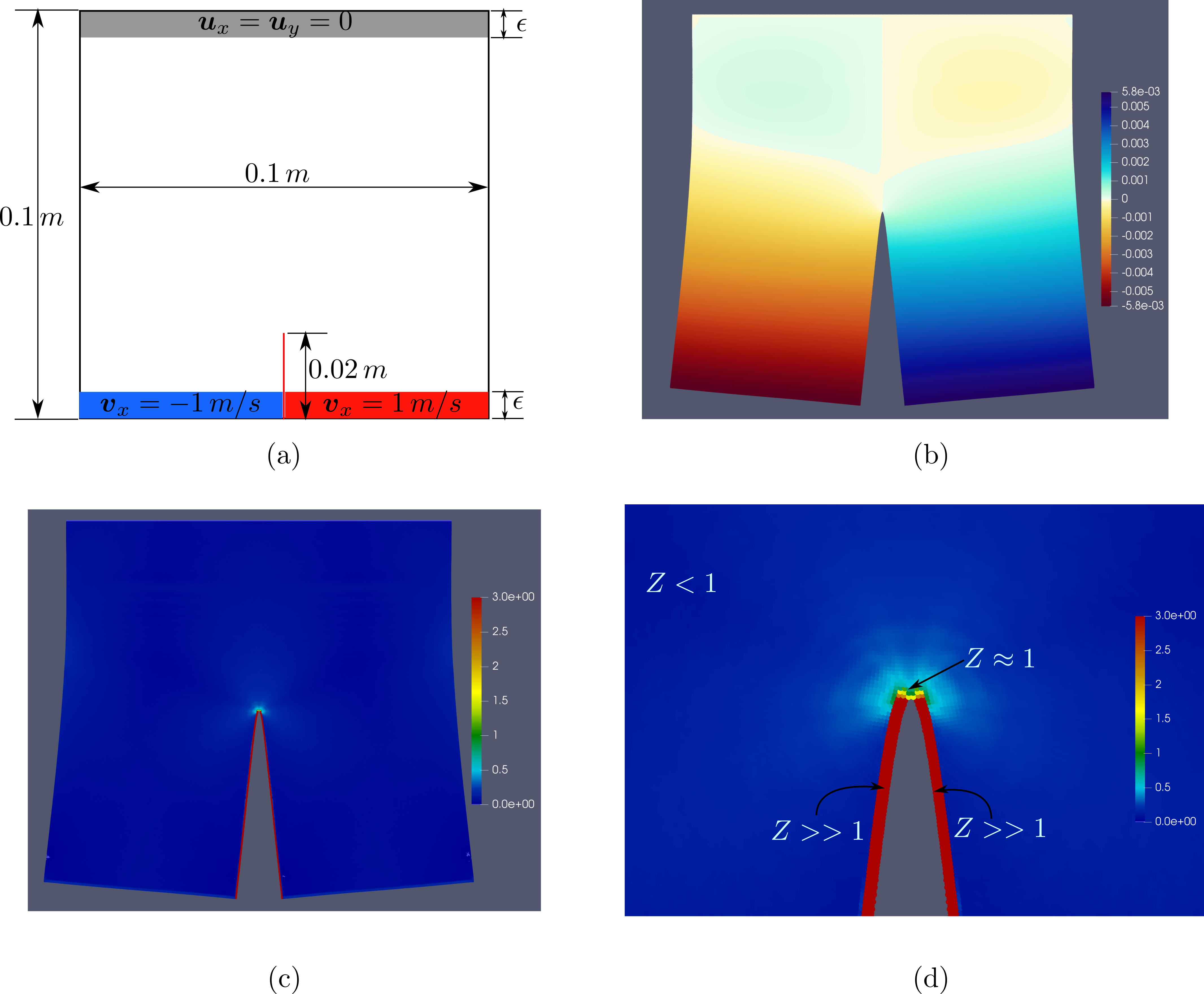
    • See figure for setup details.

  • Pre-crack: We consider vertical pre-crack of length l = 0.02 m starting from center of bottom edge, see figure above.

    • Pre-crack and fracture related methods can be found in Fracture.

  • We specify Displacement, Velocity, Force and Damage_Z as output candidates.

Mesh

We consider uniform mesh of mesh size h = $\epsilon$/4.

  • To generate uniform mesh, run Mesh with input file input_mesh.yaml. It will produce mesh.vtu which is needed to run the simulation, see input.yaml file where mesh input details are provided.

Results

We show setup, displacement, and damage plot at time t = 0.000058 seconds. Results are from paper Lipton et al 2019.

setup