Validating the state-basd elastic model (2D)
Generating the mesh
The file input_mesh.yaml in the example folder will generate the mesh as shown in the following figure.
Model
The quasi-static models as described in [1] is used to assemble the tangent stiffness matrix and obtain the solution by solving Newton steps.
Model:
Dimension: 2
Discretization_Type:
Spatial: finite_difference
Time: quasi_static
Final_Time: 1
Time_Steps: 1
Horizon: 0.5
Horizon_h_Ratio: 5
Material model
The state-based elastic material models as described in [2] is implemented for the ElasticState material.
Material:
Type: ElasticState
Density: 1200
Compute_From_Classical: true
K: 4000.0
G: 1500.0
Is_Plane_Strain: False
Influence_Function:
Type: 1
Applying boundary conditions
Displacement boundary conditions
The following code applies a fixed displacement to the first layer of nodes on the right-hand side in the first figure in both directions.
Displacement_BC:
Sets: 2
Set_1:
Location:
Line: [1.55, 1.65]
Direction: [1]
Time_Function:
Type: constant
Parameters:
- 0.0
Spatial_Function:
Type: constant
Set_2:
Location:
Line: [1.55, 1.65]
Direction: [2]
Time_Function:
Type: constant
Parameters:
- 0.0
Spatial_Function:
Type: constant
Force boundary conditions
The following code applies a external body force density to the last node on the left-hand side in the first figure.
Note that in this example we want to apply a force $F=-40N$, however, the body force density has the units $\frac{N}{mm^2}$. Thus, the force is devided by the area $1.6\times 0.1$, where $1.6$ is the length of the plate and $0.1$ is the mesh width. This results in a body force density $-250$.
Force_BC:
Sets: 1
Set_1:
Location:
Line: [-0.1, 0.05]
Direction: [1]
Time_Function:
Type: linear
Parameters:
- 1
Spatial_Function:
Type: constant
Parameters:
- -250.0
Solver
Solver:
Type: BiCGSTAB
Max_Iteration: 200
Tolerance: 1e-6
Perturbation: 1e-7
Validation
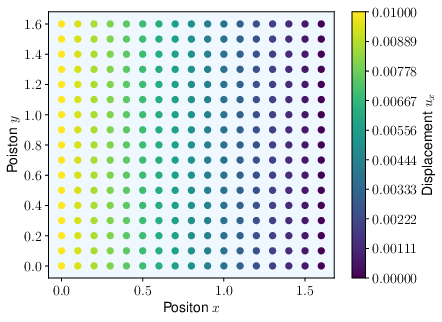
The prediction of the displacement field in $x$-direction is shown in second figure. For the derivation of the displacement field, we refer to [3].
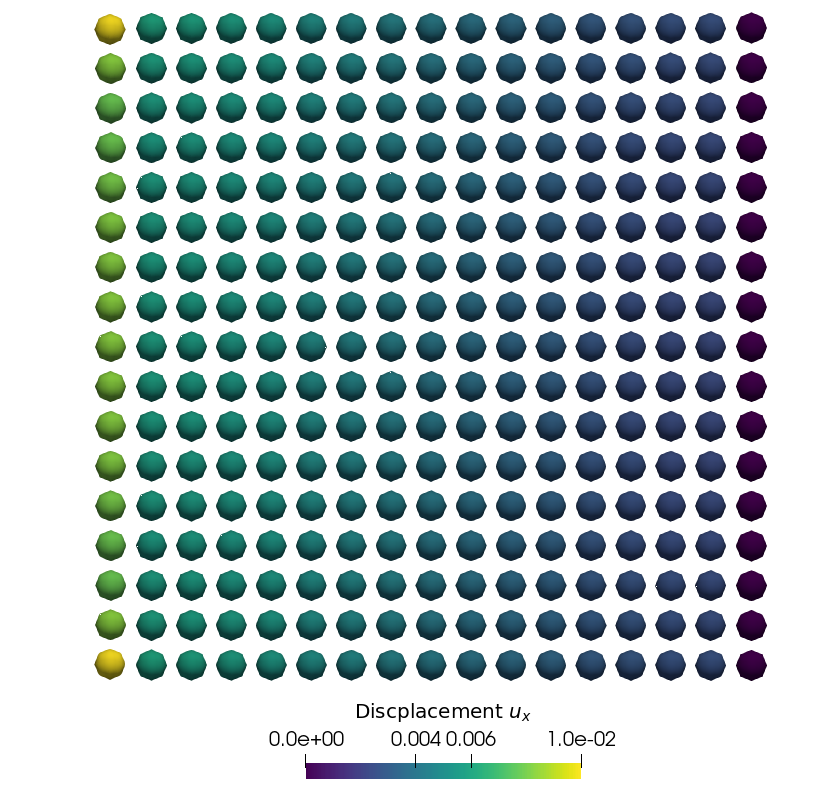
The third figure shows the obtained displacement field by the code using the above configuration.
References
- Littlewood, David J. “Roadmap for peridynamic software implementation.” SAND Report, Sandia National Laboratories, Albuquerque, NM and Livermore, CA (2015).
- Silling, Stewart A., et al. “Peridynamic states and constitutive modeling.” Journal of Elasticity 88.2 (2007): 151-184. 3.